7.1 Máquinas de Boltzmann

Las redes neuronales se pueden caracterizar por sus:

• Valores binarios o continuos.
• Transiciones determinísticas o probabilísticas.
• Conecciones unidireccionales o bidireccionales.
• Representaciones distribuidas o locales.
• Aprendizaje supervisado o no supervisado.
• Unidades ocultas o no.

La máquina de Boltzmann usa estados binarios, conecciones bidireccionales, transiciones probabilísticas y puede tener unidades ocultas.

Para ajustar los estados de las unidades individuales se usa un mecanismo de transición de estados que está regido por el algoritmo de recocido simulado.

El modelo matemático de la Máquina de Boltzmann tiene dos atributos:

1. Se puede considerar como un modelo de implementación paralela en forma masiva del algoritmo de recocido simulado.
2. Permite el diseño de un algoritmo de aprendizaje basado en conceptos relativamente simples.

Una máquina de Boltzmann se puede ver como una red de varias unidades de dos estados (prendida = 1, apagada = 0) conectadas de cierta forma. El conjunto de conecciones normalmente incluye ``auto conecciones'' (conecciones de una unidad a sí misma).

Si se tiene una conección entre dos unidades $u$ y $v$, entonces la conección entre ellas $\{u,v\}$ está prendida si: $k(u) \cdot k(v) = 1$ (donde $k(i)$ denota el estado de la unidad $i$).

Con cada conección se asocia una fuerza (número real). La fuerza es una medidad cuantitativa de lo deseable de la conección.

La fuerza de la conección $\{u,u\}$ se llama el sesgo de la unidad $u$.

Una configuración $k$ está dada por el estado global de una máquina de Boltzmann (i.e., por los estados de cada unidad).

La función de consenso asigna a cada configuración un número real dado como la suma de las fuerzas de las conecciones activadas

$$C(k) = \sum_{\{u,v\} \in C} w_{\{u,v\}} k(u) k(v)$$

.

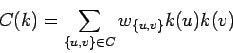
donde: $w_{u,v}$ = la fuerza de conección y $k(i)$ = la configuración de la unidad $i$.

El consenso es grande si están activadas muchas de las conecciones exitatorias (y pequeño si son las inhibitorias).

El objetivo de la máquina de Boltzmann es encontrar una configuración que alcance un máximo global (i.e., una configuración de consenso máximo).

El ajuste está determinada por una función estocástica de los estados de los vecimos y sus fuerzas de conección.

Básicamente usa el criterio de aceptación del recocido simulado.

Existen dos modelos:

• Máquinas de Boltzmann sequenciales: las unidades cambian de estado una a la vez.
• Máquinas de Boltzmann paralelas: las unidades cambian de estado simultaneamente.