7.0.1 Historia

Existió mucho desarrollo en los primeros años de la computación: McCulloch y Pitts (43), Hebb (49), Minsky (51) (primera red), Ashby (52), Rosenblatt (57) (perceptrón), Selfridge (59) (pandemonium), Widrow y Hoff (60) (adalines), Nilsson (65 - 90), Minsky y Papert (69).

Después del libro de Minsky y Papert prácticamente no se hizo nada durante los siguientes 10 años.

El resurgimiento comenzó en la decada de los 80's: Hinton y Anderson (81), Hopfield (82), Hinton y Sejnowski (83 y 86) y los dos volumens de PDP (Parallel Distributed Processing) anthology (Rumelhart et al. 86).

Una red neuronal artificial está compuesta por nodos o unidades, conectados por ligas. Cada liga tiene un peso numérico asociado. Los pesos son el medio principal para almacenamiento a largo plazo en una red neuronal, y el aprendizaje normalmente se hace sobre la actualización de pesos.

Algunas unidades están conectadas al medio ambiente externo y pueden diseñarse como unidades de entrada o salida.

Los pesos se modifican para tratar de hacer que el comportamiento entrada/salida se comporte como el del ambiente.

Cada unidad tiene un conjunto de ligas de entrada (provenientes de otras unidades) y un conjunto de ligas de salida (hacia otras unidades), un nivel de activación, y una forma de calcular su nivel de activación en el siguiente paso en el tiempo, dada su entrada y sus pesos (cada unidad hace un cálculo local basado en las entradas de sus vecinos).

En la práctica, casi todas las implementaciones de RN son en software y utilizan un control síncrono en su actualización.

Para el diseño uno debe de decidir:

• Número de unidades.
• Cómo se deben de conectar.
• Qué algoritmo de aprendizaje utilizar.
• Cómo codificar los ejemplos de entradas y salidas.

Cada unidad recibe señales de sus ligas de entradas y calcula un nuevo nivel de activación que manda a través de sus ligas de salidas.

La computación se hace en función de los valores recibidos y de los pesos.

Se divide en dos:

1. Un componente lineal, llamado la función de entrada ($in_{i}$), que calcula la suma de los valores de entrada.
2. Un componente no lineal, llamado función de activación ($g$), que transforma la suma pesada en una valor final que sirve como su valor de activación ($a_{i}$).

Normalmente, todas las unidades usan la misma función de activación.

La suma pesada es simplemente las entradas de activación por sus pesos correspondientes:

$$in_i = \sum_j w_{j,i} a_j = {\bf {w}_i \cdot {a}_i }$$

${\bf {w}_i}$: vector de los pesos que llegan a la unidad $i$
${\bf {a}_i}$: vector de los valores de activación de las entradas a la unidad $i$

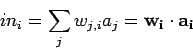
El nuevo valor de activación se realiza aplicando una función de activación $g$:

$$a_i \leftarrow g(in_i) = g( \sum_j w_{j,i} a_j )$$

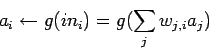
Se obtienen modelos diferentes cambiando $g$. Las opciones más comunes son (ver figura 7.1):

Figura 7.1: Funciones de activación comunes para Redes Neuronales.

• Función escalón:
  
  $$escalon_{t}(x)=\left\{ \begin{array}{ll} 1, & \mbox{ si }x\geq t \\ 0, & \mbox{ si }x<t \end{array}\right.$$
  
  

• Signo:
  
  $$signo(x)=\left\{ \begin{array}{ll} +1, & \mbox{ si }x\geq 0 \\ -1, & \mbox{ si }x<0 \end{array}\right.$$
  
  

• Sigmoide:
  
  $$sigmoide(x)=\frac{1}{1+e^{-x}}$$
  
  

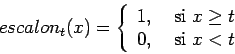
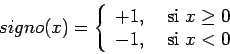
Una de las motivaciones iniciales en el diseño de unidades individuales fué la representación de funciones Booleanas básicas (McCulloch y Pitts, '43).

Esto es importante, porque entonces podemos usar estas unidades para construir una red que compute cualquier función Booleana.

Los modelos de redes neorunales principalmente usados para resolver problemas de optimización son:

• Las máquinas de Boltzmann.
• Las redes de Hopfield.
• Los mapas auto-organizativos (SOM).