El problema del Max Cut es el siguiente: Dado un grafo ![]() con
pesos positivos en los arcos, el problema consiste en enconrar una
partición de
con
pesos positivos en los arcos, el problema consiste en enconrar una
partición de ![]() en conjuntos disjuntos
en conjuntos disjuntos ![]()
![]() , al que la suma
de los pesos de los arcos que tienen un extremo en
, al que la suma
de los pesos de los arcos que tienen un extremo en ![]() y el otro en
y el otro en
![]() sea máxima.
sea máxima.
Los pesos son simétricos (
![]() ) y podemos definir una
variable
) y podemos definir una
variable ![]() binaria como sigue:
binaria como sigue:
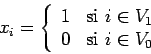
Entonces el problema Max Cut lo podemos formular como sigue:
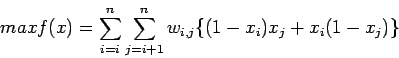
Sea ![]() la suma de los pesos de todos los nodos que inciden en el
nodo
la suma de los pesos de todos los nodos que inciden en el
nodo ![]() , i.e.,
, i.e.,
![]() . Si
. Si ![]() son las
conecciones de sesgo (auto-conecciones) y
son las
conecciones de sesgo (auto-conecciones) y ![]() son las conecciones de
peso (entre nodos), una función de consenso que preserva el orden
es:
son las conecciones de
peso (entre nodos), una función de consenso que preserva el orden
es:
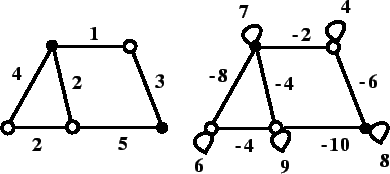
En la figure 7.5 se ve un grafo de ejemplo y su máquina de Boltzmann correspondiente.
 |