Dada una máquina de Boltzmann en una configuración ![]() , la
configuración vecina
, la
configuración vecina ![]() se define como la configuración que se
obtiene del estado
se define como la configuración que se
obtiene del estado ![]() al cambiar el estado de una unidad
al cambiar el estado de una unidad ![]() (de 0 a
1 o viceversa).
(de 0 a
1 o viceversa).
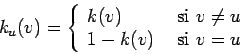
La vecindad se define como todos los estados de configuraciones
vecinas a la configuración ![]() .
.
Si ![]() denota todas las conecciones que inciden en la unidad
denota todas las conecciones que inciden en la unidad ![]() (eliminando
(eliminando ![]() ), y sea
), y sea
![]() . La diferencia de
consenso entre las configuraciones
. La diferencia de
consenso entre las configuraciones ![]() y
y ![]() se denota como:
se denota como:
Dado que la contribución de las conecciones en ![]() al consenso es
igual para
al consenso es
igual para ![]() que para
que para ![]() , se obtiene:
, se obtiene:
![\begin{eqnarray*}
\triangle C_k(u) & = & \mbox{ } \left [ k_u(u)\sum_{\{u,v\} \i...
...{\{u,v\} \in C_u} w_{\{u,v\}} k(v)
+ k^2(u) w_{\{u,u\}} \right ]
\end{eqnarray*}](img350.png)
que nos da al cambiar ![]() por
por ![]() y desarrollar:
y desarrollar:
![\begin{displaymath}\triangle C_k(u) = (1 - 2k(u)) \left [ \sum_{\{u,v\} \in C_u}
w_{\{u,v\}} k(v) + w_{\{u,u\}} \right ] \end{displaymath}](img353.png)
Básicamente lo que dice es que el efecto del consenso, resultando de
cambiar el estado de la unidad ![]() , está completamente determinado
por los estados de los vecinos y de sus fuerzas de conección.
, está completamente determinado
por los estados de los vecinos y de sus fuerzas de conección.
Por lo mismo una unidad puede ser evaluada localmente, lo cual es muy importante por su potencial paralelización.
Una configuración de máximo local es aquella en donde no se puede aumentar cambiando transiciones de un solo estado.
Ejemplo: Las figuras 7.2 y 7.3 muestra un ejemplo de una máquina de Boltzmann.
Como en el caso de recocido simulado, se puede usar el concepto de cadenas de Markov para describir las transiciones de estado de una máquina de Boltzmann.
En una máquina secuencial consiste de dos pasos:
También se introduce un parámetro de control ![]() , que determina la
probabilidad de aceptación de una transición.
, que determina la
probabilidad de aceptación de una transición.
La probabilidad de transición ![]() de la configuración
de la configuración ![]() a
la
a
la ![]() se define como:
se define como:
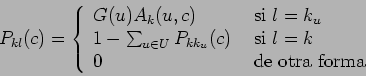
donde ![]() denota la probabilidad de generar una transición de
estado de la unidad
denota la probabilidad de generar una transición de
estado de la unidad ![]() ,
, ![]() denota la probabilidad de
aceptación de la transición, y
denota la probabilidad de
aceptación de la transición, y ![]() denota el parámetro de
control.
denota el parámetro de
control.
La probabilidad de generación se escoge normalmente de forma uniforme
sobre las posibles unidades e independiente de la configuración ![]() o
el parámetro de control
o
el parámetro de control ![]() .
.
La probabilidad de aceptación se escoge como:
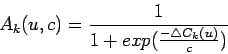
Esto difiere un poco de la probabilidad de aceptación del algoritmo de recocido simulado, pero en realidad muy poco. Ambas probabilidades dan la misma distribución estacionaria y tienen las mismas propiedades de convergencia.
La figure 7.4 muestra esta función para varios
valores de ![]() .
.
Se puede probar que las máquinas de Boltzmann convergen asintóticamente al conjunto de configuraciones globales óptimas basandose en la existencia de una distribución estacionaria.
Como en recocido simulado, se tiene que hacer una aproximación en tiempo finito al especificar los parámetros que determinan el esquema de enfriamiento.
El esquema es básicamente el mismo que se sigue para el recocido simulado.
Pesos positivos (negativos) en las auto-conecciones indican una tendencia a estar las unidades prendidas (apagadas) y entre las conecciones con otras unidades indican que deben de estar las dos unidades conectadas prendidas.