El algoritmo de recocido simulado puede ser modelado matemáticamente usando cadenas de Markov.
Una cadena de Markov es una secuencia de eventos, donde la probabilidad del resultado de un evento depende sólo del resultados del evento anterior.
Sea ![]() una variable estocástica que denota el resultado del
una variable estocástica que denota el resultado del
![]() -ésimo evento. Entonces la transición de probabilidad en el
-ésimo evento. Entonces la transición de probabilidad en el
![]() -ésimo evento para cada par
-ésimo evento para cada par ![]() de resultados se define como:
de resultados se define como:
La matriz ![]() cuyos elementos están dados por la fórmula de
arriba se llama la matriz de transición.
cuyos elementos están dados por la fórmula de
arriba se llama la matriz de transición.
Denotemos a ![]() como la probabilidad del resultado
como la probabilidad del resultado ![]() en el
en el
![]() -ésimo evento, osea:
-ésimo evento, osea:
![]() .
.
Entonces ![]() se define como:
se define como:
Mencionemos algunas propiedades de cadenas de Markov. Una cadena de Markov se dice:
En recocido simulado, un evento corresponde a una transición y los resultados posibles corresponden al conjunto de soluciones posibles.
Las probabilidades de transición del algoritmo de recocido simulado están definidas como:
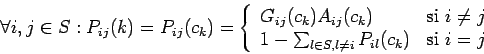
donde:
![]() denota la probabilidad de generación (la
probabilidad de generar una solución
denota la probabilidad de generación (la
probabilidad de generar una solución ![]() a partir de una solución
a partir de una solución
![]() ).
).
donde
![]() , para toda
, para toda ![]() .
.
![]() denota la probabilidad de aceptación (la probabilidad
de aceptar la solución
denota la probabilidad de aceptación (la probabilidad
de aceptar la solución ![]() una vez que fué generada a partir la
solución
una vez que fué generada a partir la
solución ![]() ).
).
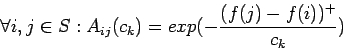
Lo que queremos probar es que, bajo ciertas condiciones, el algritmo
de recocido simulado converge asintóticamente al conjunto de
soluciones óptimas, i.e.,:
Una parte escencial para la prueba de convergencia es la existencia de una distribución estacionaria única. Tal distribución existe sólo si se cumplen ciertas condiciones en la cadena de Markov asociada al algoritmo.
Una distribución estacionaria de una cadena de Markov finita con
matriz de transición ![]() se define como un vector q cuyo
se define como un vector q cuyo
![]() -ésimo componente está dado por:
-ésimo componente está dado por:
Si existe esa distribución estacionaria, entonces,
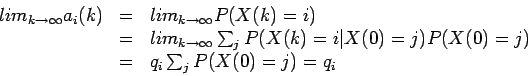
Teniamos que:
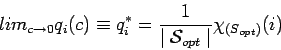
Por lo que:
Aunque no es propiamente una prueba, lo de arriba indica algunas de las ideas principales que se usan en la prueba de convegencia.
Todas las pruebas usan la condición de reversibilidad o
también llamada de balance detallado. Lo que dice es que si
tenemos una matriz de transición ![]() asociada a una cadena de
Markov finita, irreducible, aperiódica y homogénea. Entonces una
distribución es estacionaria para la cadena de Markov si satisface:
asociada a una cadena de
Markov finita, irreducible, aperiódica y homogénea. Entonces una
distribución es estacionaria para la cadena de Markov si satisface:
Las pruebas de convergencia nos dicen que el algoritmo de recocido simulado requiere un número infinito de transiciones para aproximarse lo suficiente a una distribución estacionaria en cada temperatura.
Esto involucraría la generación de secuencias infinitas para
valores descendientes del parámetro de control ![]() .
.
Sin embargo, podemos formular el algoritmo de recocido simulado como una secuencia de cadenas de Markov de longitud finita que converge al conjunto de soluciones óptimas si el enfriamiento se hace lo suficientemente lento.
El proceso se puede describir mediante la combinación de cadenas de Markov homogeneas en una solo cadena de Markov no-homogena. Dicho de otra forma, la secuencia de cadenas de Markov homogenas infinitamente largas se reducen a una sola cadena de Markon no homogenas infinita.