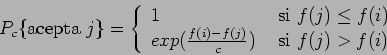
La analogía es la siguiente:
El algoritmo de recocido simulado se puede ver como una iteración de algoritmos de Metrópolis (ver tabla 6.2).
Si se baja la temperatura suficientemente lento se puede alcanzar el equilibrio térmico en cada temperatura. Esto se hace mediante la generación de varias transiciones en cada temperatura.
Se puede demostrar que bajando suficientemente lento el parámetro asociado a la temperatura y generando suficientes transiciones en cada temperatura se puede alcanzar la configuración óptima.
La probabilidad de aceptación se expresa como sigue:
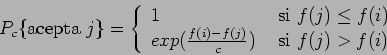
donde
![]() denota el parámetro de control.
denota el parámetro de control.
Una transición consiste en (i) aplicación del mecanismo de generación, y (ii) aplicación del mecanismo de aceptación.
Inicialmente valores grandes de ![]() aceptan cualquier estado. Al
tender
aceptan cualquier estado. Al
tender ![]() a cero, se dejan de aceptar estados.
a cero, se dejan de aceptar estados.
La velocidad de convergencia del algoritmo está determinada por ![]() y
y ![]() .
.
Búqueda local se puede ver como quenching.
Un sistema físico de muchas particulas puede verse como un ``ensamble'' estadístico.
Si el ensable es estacionario, el cual se logra en equilibrio
térmico, su densidad es función de la energía del sistema y la
probabilidad de estar en un estado ![]() con energía
con energía ![]() está dado
por la distribución de Boltzmann.
está dado
por la distribución de Boltzmann.
Dada una instancia de un problema combinatorio y una estructura de
vecinos adecuada, después de un número de transiciones
suficientemente largo para un valor fijo de ![]() , aplicando el criterio
de aceptación, el algoritmo de recocido simulado encuentra una
solución
, aplicando el criterio
de aceptación, el algoritmo de recocido simulado encuentra una
solución ![]() con probabilidad igual a:
con probabilidad igual a:
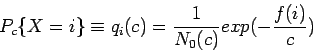
donde ![]() es una variable estocástica denotando la solución actual y
es una variable estocástica denotando la solución actual y
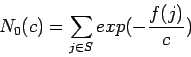
Dada una instancia de un problema de optimización combinatoria, una
estructura de vecindad adecuada y una distribución estacionaria
equivalente a la distribución de Boltzmann, entonces:
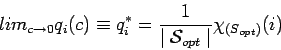
donde
![]() denota el conjunto de soluciones óptimas
globales, y
denota el conjunto de soluciones óptimas
globales, y ![]() es la función característica definida
como:
es la función característica definida
como:
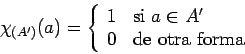
El resultado es importante porque garantiza una convergencia
asintótica hacia el conjunto de soluciones óptimas del algoritmo de
recocido simulado bajo la condición que la distribución estacionaria
se obtenga para cada valor de ![]() .
.
La probabilidad de encontrar la solución óptima incrementa
monotónicamente al decrementar ![]() .
.