6.5 Aproximaciones

Como en la práctica no se puede garantizar llegar a la solución óptima se hacen aproximaciones con longitud de transiciones finitas y número de descensos del parámetro de control finito, que arrojan soluciones sub-óptimas.

Se requiere definir un mecanismo de enfriamiento que especifique:

• Una secuencia finita de valores para el parámetro de control: (i) un valor inicial 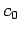$c_0$, (ii) una función de decremento, y (iii) un valor final (condición de paro).
• Un número finito de transiciones para cada valor del parámetro de control (longitud finita de cada cadena de Markov).

Una idea clave en las aproximaciones es llegar a un cuasi-equilibrio (esto es, si la distribución de probabilidad de las soluciones después de un número finito de eventos es ``suficientemente cerca'' con la distribución estacionaria).

Existe un balance entre la longitud de las cadenas de Markov y los decrementos realizados en el parámetro de control.

Decrementos largos en 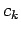$c_k$ requieren muchas transiciones para restablecer el cuasi-equilibrio y viceversa.

Mecanismo de enfriamiento propuesto por Kirkpatrick:

• Valor inicial del parámetro de control: empezar con un entero positivo pequeño e irlo multiplicando por un factor mayor a 1 hasta que las transiciones generadas sean casi todas aceptadas.
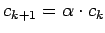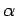• Decremento del parámetro de control: $c_{k+1} = \alpha \cdot c_k$, donde $\alpha$ es una constante cercana a 1 (0.8 - 0.99).
• Valor final del parámetro de control: terminar cuando la solución obtenida permancece igual en un número determinado de cadenas consecutivas.
• Longitud de las cadenas de Markov: hacer una longitud (L) fija (de otra forma 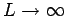$L \rightarrow \infty$ cuando $c_k \rightarrow 0$).

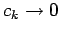Se han propuesto varios esquemas de enfriamiento en la literatura.