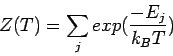La idea principal puede verse en la tabla 6.1
(Metropolis et al. 1953) donde ![]() denota la temperatura y
denota la temperatura y ![]() la
constante de Boltzmann.
la
constante de Boltzmann.
Lo que hace el algoritmo de Metropolis es generar un vecino,
calcularle su energía (i.e., función de costo en problemas de
optimización) y aceptar ese vecino si tiene menor energía o
aceptarlo con mayor energía pero con cierta probablidad que
depende de la temperatura (![]() ).
).
Se puede probar que si se realiza este proceso durante muchas transiciones se puede llegar a lo que se conoce como un equilibrio térmico.
El equilibrio térmico está caracterizado por la distribución de Boltzmann.
La distribución da la probabilidad de que el sólido
esté en el estado ![]() con energía
con energía ![]() a temperatura
a temperatura ![]() y
está dada por:
y
está dada por:
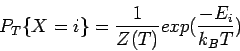
donde ![]() es la variable estocástica denotando el estado actual del
sólido, y
es la variable estocástica denotando el estado actual del
sólido, y ![]() es la función de partición definida como:
es la función de partición definida como: