3.6 Estrategias de Juego

Progressive/iterative deepening: explorar por niveles.

Si: $b$ = branching factor y $d$ = profundidad: En general el número de nodos evaluados al final es: $b^d$.

El número de nodos en el resto del árbol es:

$$\sum_{i=0}^{d - 1} b^i = \frac{b^d - 1}{b - 1}$$

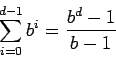
La razón entre ellos es:

$$b^d \frac{b - 1}{b^d - 1} \approx b - 1$$

i.e., con profundidad de 16 el costo total es $\frac{1}{15}$ del costo normal lo cual es bastante bajo.

Heuristic Pruning: ordenar los nodos con respecto a su función de evaluación y variar la profundidad de exploración (mayor/menor). Sin embargo con sólo esta estrategia no habría sacrificios de damas en ajedrez.

Heuristic Continuation: continuar caminos que por heurísticas se consideran importantes (e.g., el rey peligra, se va a perder una pieza, un peón puede coronar, etc.), para tratar de evitar el efecto horizonte (no siempre se puede).

Quiescence Search: En principio, no se debería de aplicar la función de evaluación en posiciones en donde no se esperan cambios fuertes en el valor de la función de evaluación.

A esto, se le llama quiescence search y a veces se restringe sólo a algunos tipos particulares de movidas (e.g., capturas).

Todas las metodologías asumen que la decisión de la jugada mejora con la profundidad de la búsqueda.

Se ha mostrado que funciona bien en juegos y ésto se cuestiona poco. De hecho se cree que el nivel extra de exploración en ajedrez mejora en 200 el puntaje de la máquina.

Sin embargo, se ha mostrado que el nivel discriminatorio decrece apreciablemente en cada nivel.

Si la función de evaluación se mantiene igual en todos los niveles de juego, entre más buscamos a profundidad, peor es nuestra evaluación.

Porqué no ocurre en los juegos?

Los juegos comunes no son uniformes, están llenos de ``trampas'' que son detectadas al buscar a profundidad.

Sin embargo, no se debe de perder de vista la detereoridad del algoritmo.

Algo muy usado en juegos (además de guardar aperturas y finales de juego) son las transposition tables. Esto es, guardar información de nodos recorridos para evitar recorrerlos otra vez.

Existen muchas otras estrategias: En B* (Berlinger 79), cada nodo tiene una evaluación pesimista y una optimista. Un nodo deja de ser explorado cuando su estimación optimista es más baja que todas las pesimistas de sus rutas alternas.

Líneas de investigación: usar meta-razonamiento y combinar planeación con búsqueda.