11.1.2 Recompensa diferida y modelo Markoviano

En general, las acciones del agente determinan, no sólo la recompensa inmediata, sino también (por lo menos en forma probabilística) el siguiente estado del ambiente.

Los problemas con refuerzo diferido se pueden modelar como procesos de decisión de Markov (MDPs).

El modelo es Markoviano si las transiciones de estado no dependen de estados anteriores.

En aprendizaje por refuerzo se asume que se cumple con la propiedad Markoviana y las probabilidades de transición están dadas por:

$${\cal P}_{ss'}^a = Pr\{s_{t+1} = s' \mid s_t = s, a_t = a \}$$

El valor de recompensa esperado es:

$${\cal R}_{ss'}^a = E\{ r_{t+1} \mid s_t = s, a_t = a, s_{t+1} = s'\}$$

Lo que se busca es estimar las funciones de valor. Esto es, qué tan bueno es estar en un estado (o realizar una acción).

La noción de ``qué tan bueno'' se define en términos de recompensas futuras o recompensas esperadas.

La política $\pi$ es un mapeo de cada estado $s \in S$ y acción $a \in {\cal A}(s)$ a la probabilidad $\pi(s,a)$ de tomar la acción $a$ estando en estado $s$. El valor de un estado $s$ bajo la política $\pi$, denotado como $V^{\pi}(s)$, es el refuerzo esperado estando en estado $s$ y siguiendo la política $\pi$.

Este valor esperado se puede expresar como:

$$V^{\pi}(s) = E_{\pi} \{ R_t \mid s_t = s\} = E_{\pi} \left\{ \sum_{k=o}^{\infty} \gamma^k r_{t+k+1} \mid s_t = s \right\}$$

y el valor esperado tomando una acción $a$ en estado $s$ bajo la política $\pi$ ($Q^{\pi}(s,a)$):

$$Q^{\pi}(s,a) = E_{\pi} \{ R_t \mid s_t = s, a_t = a\} = E_{\p... ...=o}^{\infty} \gamma^k r_{t+k+1} \mid s_t = s, a_t = a \right\}$$

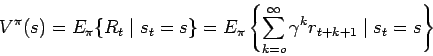
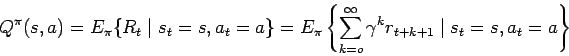
Las funciones de valor óptimas se definen como:

$$V^*(s) = max_{\pi} V^{\pi}(s) \mbox{ y } Q^*(s,a) = max_{\pi} Q^{\pi}(s,a)$$

Las cuales se pueden expresar como las ecuaciones de optimalidad de Bellman:

$$V^*(s) = max_{a} \sum_{s'} {\cal P}_{ss'}^a [ {\cal R}_{ss'}^a + \gamma V^*(s') ]$$

y

$$Q^*(s,a) = \sum_{s'} {\cal P}_{ss'}^a [ {\cal R}_{ss'}^a + \gamma V^*(s') ]$$

o

$$Q^*(s,a) = \sum_{s'} {\cal P}_{ss'}^a [ {\cal R}_{ss'}^a + \gamma \mbox{max}_{a'} Q^*(s',a') ]$$