Dado un estado ![]() y una acción
y una acción
![]() , el agente recibe una recompensa
, el agente recibe una recompensa ![]() y se mueve a
un nuevo estado
y se mueve a
un nuevo estado ![]() .
.
El mapeo de estados a probabilidades de seleccionar una acción
particular es su política (![]() ). Aprendizaje por refuerzo
especifica cómo cambiar la política como resultado de su
experiencia.
). Aprendizaje por refuerzo
especifica cómo cambiar la política como resultado de su
experiencia.
No trata de maximizar la recompensa inmediata, sino la recompensa a largo plazo (acumulada).
La recompensa debe de mostrar lo que queremos obtener y se calcula por el ambiente.
Si las recompensas recibidas después de un tiempo ![]() se denotan
como:
se denotan
como: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , lo que queremos es
maximizar lo que esperamos recibir de recompensa (
, lo que queremos es
maximizar lo que esperamos recibir de recompensa (![]() ) que en el
caso más simple es:
) que en el
caso más simple es:
Si se tiene un punto terminal se llaman tareas episódicas, si
no se tiene se llaman tareas continuas. En este último caso,
la fórmula de arriba presenta problemas, ya que no podemos hacer el
cálculo cuando ![]() no tiene límite.
no tiene límite.
Podemos usar una forma alternativa en donde se van haciendo cada vez
más pequeñas las contribuciones de las recompensas más lejanas:
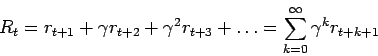
Si ![]() se trata sólo de maximizar tomando en cuenta las
recompensas inmediatas.
se trata sólo de maximizar tomando en cuenta las
recompensas inmediatas.
En general, podemos pensar en los siguientes modelos:
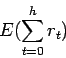
Este modelo se puede usar de dos formas: (i) política no
estacionaria: donde en el primer paso se toman los ![]() siguientes
pasos, en el siguiente los
siguientes
pasos, en el siguiente los ![]() , etc., hasta terminar. El problema
principal es que no siempre se conoce cuántos pasos considerar. (ii)
receding-horizon control: siempre se toman los siguientes
, etc., hasta terminar. El problema
principal es que no siempre se conoce cuántos pasos considerar. (ii)
receding-horizon control: siempre se toman los siguientes ![]() pasos.
pasos.
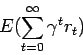
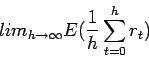
En general, se utiliza la de horizonte infinito.