9.5 Puntos a considerar en GA

• Codificación de los parámetros de un problema.

  Dentro de la codificación a veces se usan codificaciones que tengan la propiedad de que números consecutivos varíen a lo más en un bit (e.g., codificación de Gray).

  En la codificación se busca idealmente que todos los puntos estén dentro del espacio de solución (sean válidos).

  Tradicionalmente se buscan representaciones que favorescan los esquemas cortos de bajo orden.

  Pueden existir problemas de interdependencia (problemas para los GA si existe mucha y es preferible usar otro método si es casi nula).

• Función de aptitud.

  Es la base para determinar que soluciones tienen mayor o menor probabilidad de sobrevivir.

  Se tiene que tener un balance entre una función que haga diferencias muy grandes (y por lo tanto una convergencia prematura) y diferencias muy pequeñas (y por lo tanto un estancamiento).

• Criterios de tamaño de la población.

  Balance entre una población muy pequeña (y por lo tanto convergencia a máximo local) y una población muy grande (y por lo tanto requerimiento de muchos recursos computacionales).

  Los primeros intentos de tratar de estimar el tamaño de población óptimo basados en el teorema de esquemas resultaban en crecimiento exponenciales de la población con respecto al tamaño de gen.

  Experimentalmente se vió que esto no es necesario y se buscó el tamaño mínimo para poder alcanzar todos los puntos en el espacio de búsqueda.

  Se requiere solo que existe al menos cada una de las posibles instancias de los alelos en el conjunto de genes. Para genes binarios, la probabilidad de que existe al menos un alelo en cada punto es:
  

  $$P_2 = (1 - (1/2)^{M-1})^l$$
  
  
  donde $M$ es el tamaño de la población y $l$ es el tamaño del gen.

  Esto sugiere que con poblaciones de tamaño $O(log l)$ es suficiente.

  Normalmente las poblaciones se seleccionan aleatoriamente, sin embargo, esto no garantiza una selección que nos cubra el espacio de búsqueda uniformemente.

  Se pueden introducir mecanismos más sofisticados para garantizar diversidad en la población.

  Aunque normalmente se elige una población de tamaño fijo, también existen esquemas de poblaciones de tamaño variable.

• Criterio de selección.

  Individuos son copiadas de acuerdo a su evaluación en la función objetivo (aptitud). Los más aptos tienen mayor probabilidad a contribuir con una o más copias en la siguiente generación (se simula selección natural).

  Se puede implementar de varias formas, sin embargo, la más común es la de simular una ruleta, donde cada cadena tiene un espacio en ella proporcional a su valor de aptitud.

  
  

  $$Pr(h) = \frac{Aptitud(h)}{\sum_{j=1}^{N} Aptitud(h_j)}$$
  
  

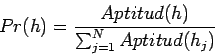
  En lugar de seleccionar uno a la vez, se pueden generar $N$ selecciones teniendo en la ruleta $N$ apuntadores que estan separados uniformemente, por lo que un giro en la ruleta nos porporciona $N$ individuos. A esto se le conoce como stochastic universal selection.

  Otra alternativa es usar selección por torneo. Se seleccionan aleatoriamente N individuos que compiten entre sí seleccionando el mejor. En esta alternativa el mejor individuo siempre es seleccionado.

  Una ventaja de este esquema es que solo necesitamos comparar si un gen es mejor que otro, por lo que posiblemente no tenemos que evaluar la función de aptitud.

  Sin embargo, haciendo muestreo con reemplazo, existe una probabilidad de aproximadamente 0.368 ( $\approx e^{-1}$) de que un gen no sea seleccionado.

  Finalmente, el otro tipo de selección es por ranqueo. Simplemente se ordenan los genes. La probabilidad de seleccionar un gen ranqueado como el $k$-ésimo ($P(k)$), en el caso de ranqueo lineal, es:
  

  $$P(k) = \alpha + \beta k$$
  
  
  donde $\alpha$ y $\beta$ son constantes y
  
  $$\sum_{k=1}^M (\alpha + \beta k) = 1$$
  
  

• Nueva población.

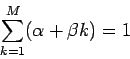
  Se pueden seleccionar individuos de la población actual, generar una nueva población y reemplazar con ella completamente a la población que se tenia (esquema generacional).

  También a veces se mantienen los $N$ mejores individuos de una población a la siguiente (esto parece ser la mejor opción). Si se conserva solo el mejor individuo se llama estrategia elitista, si se mantiene un subconjunto se habla de poblaciones traslapadas.

• Criterio de paro.

  Normalmente cuando un porcentaje alto de la población converge a un valor o después de un número fijo de evaluaciones en la función de aptitud. Si con ese valor no se llega a la medida esperada (si es que se conoce) o simplemente para tratar de mejorar la solución, entonces se toma una pequeña proporción y se inyecta ``diversidad genética'' (se generan aleatoriamente nuevos individuos), o inclusive se reemplaza completamente la población.

• Operadores genéticos.

  Normalmente se hace cruza seguida de mutación, pero se podría hacer una o la otra, por ejemplo.

  Algunas personas proponen hacer mucha cruza al principio e incrementar la mutación conforme pasa el tiempo.

  • Cruce: tiene una alta probabilidad de ser utilizado y es considerado como el más importante dentro de los AG. Permite la generación de nuevos individuos tomandos características de individuos padres. Consiste en seleccionar dos individuos después del proceso de selcción, determinar una posición de cruce aleatoria e intercambiar las cadenas entre la posición inicial y el punto de cruce y el punto de cruce y la posición final.

    Existen diferentes tipos de cruza. (i) Cruza simple: un solo punto de cruza (una máscara de 1's seguida de 0's), (ii) cruza de dos puntos y (iii) cruza uniforme (generando una máscara con 1's y 0's siguiendo una distribución de Bernoulli).

    Existe evidencia empírica que sugiere que cruza en un punto no es la mejor opción.

  • Mutación: tiene baja probabilidad de ser utilizado y permite introducir nueva información no presente en la población. Opera sobre un solo individuo, determina una posición y la invierte con cierta probabilidad. Permite salir de máximos locales.

    En lugar de generar un número aleatorio para cada alele y ver si se muta o no, se puede generar un número que nos de el número de mutaciones a realizar (M) y simplemente generar M números aleatorios entre 1 y el tamaño del gen.

    Lo único que falta por determinar es que valor usar cuando existan más de dos posibles valores.

  • Inversión: tiene baja probabilidad. Incrementa la capacidad de exploración. Permite generar cadenas que serían difíciles de obtener con los otros dos operadores. Opera en un individuo, determina dos posiciones dentro de la cadena e invierte la subcadena.

  • Existen más...

Vamos a ver tres formas de uso común de algortimos genéticos: (i) cambio de parámetros (ii) cambio de estructuras de datos (iii) cambio de programas