 |
Es una alternativa para formar clusters o grupos, a partir de datos, cuando se conoce el número de grupos a formar.
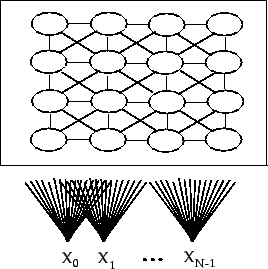
Se ajustan los pesos de un vector de entrada a nodos de salida organizados en una malla bidimensional (ver figura 7.6).
Se requiere definir una vecindad alrededor de cada nodo, la cual se va reduciendo con el tiempo (ver figura 7.7).
Las entradas se normalizan y se procesan una por una (ver tabla 7.2).
Los resultados dependen del orden de los ejemplos para poco datos.
La aplicación a problemas de optimización se hace normalmente escogiendo una topología en los nodos de salida particular que reflejen la posible solución del problema a resolver.
Posiblemente la real ventaja de usar estas redes en lugar de alguna de las metaheurísticas propuestas en la literatura, es su facilidad de ser implementadas en hardware.