Las redes de Hopfield son probablemente las mejor entendidas de redes
recurrentes. Tienen conecciones bidireccionales con pesos
simétricos (i.e.,
![]() ). Todas las unidades son
tanto unidades de entrada como de salida. La función de
activación es la función signo, y los valores de
activación pueden ser sólo
). Todas las unidades son
tanto unidades de entrada como de salida. La función de
activación es la función signo, y los valores de
activación pueden ser sólo ![]() .
.
Una red de Hopfield funciona como una memoria asociativa. Despues de entrenarse con un conjunto de ejemplos, un nuevo estímulo causa la red a ``asentarse'' en un patrón de activación correspondiente al ejemplo de entrenamiento que se parece más al nuevo estímulo.
Esto es, se alimenta un patrón de entrada y se observa su salida. La salida se vuelve a alimentar a la red y se ve la nueva salida. Este proceso continua hasta que no hay cambios en la salida.
Uno de los resultados teóricos interesantes es que una red de
Hopfield puede almacenar en forma confiable hasta: ![]() ejemplos
de entrenamiento (donde
ejemplos
de entrenamiento (donde ![]() es el número de unidades de la red).
es el número de unidades de la red).
Cada neurona tiene un estado interno ![]() y uno externo
y uno externo ![]() . Los
valores internos son continuos y los externos binarios. La
actualización y relación entre estos valores es:
. Los
valores internos son continuos y los externos binarios. La
actualización y relación entre estos valores es:
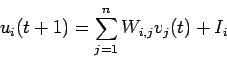
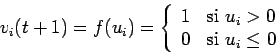
donde ![]() es una constante externa de entrada a la neurona
es una constante externa de entrada a la neurona ![]() y
y
![]() es la función de transferencia entre los estados internos y
externos.
es la función de transferencia entre los estados internos y
externos.
Las neuronas se actualizan es forma aleatoria.
La siguiente función de energía es la que se minimiza, esto es, el mínimo local de la función de energía corresponde con la energía del patrón almacenado.
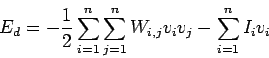
Las funciones de actualización hacen un gradiente decendiente en la función de energía.
Tambén existe una versión continua de redes de Hopfield..
Para aplicarla a un problema de optimización combinatoria, se tienen que seleccionar pesos y entradas externas que representen en forma adecuada la función a minimizar.
En el caso de TSP, se puede hacer la siguiente formulación:

La función objetivo y las restricciones las podemos expresar como:
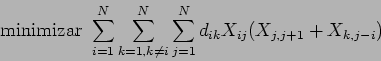
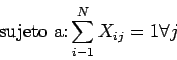
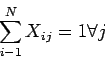
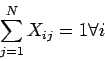
Para aplicarlo, las restricciones del problema se añaden a la
función objetivo.
Una posible formulación para ![]() ciudades es:
ciudades es:
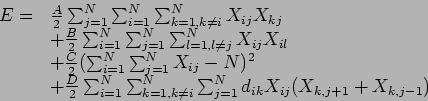
Los primeros dos términos dicen que no puede existir más de un
``1'' por columna y por renglón respectivamente, el tercer
término aseguro que existan ![]() elementos ``prendidos'' en la
matríz de solución y el último término minimiza la
longitud del circuito.
elementos ``prendidos'' en la
matríz de solución y el último término minimiza la
longitud del circuito.
En la formulación original de Hopfield y Tank (85) usaron los
siguientes valores: ![]() y
y ![]() .
.
Para ponerlo en términos de la función de energía de
Hopfield, introducimos la función delta de Kronecker:
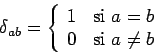
y expresamos la función de energía como:
![\begin{displaymath}
\begin{array}{lll}
E = & - \frac{1}{2} \sum_{i=1}^N \sum_{j=...
...{i=1}^N \sum_{j=1}^N [C N] X_{ij} + \frac{C N^2}{2}
\end{array}\end{displaymath}](img406.png)
Lo que nos deja (ignorando la constante):
Una vez hecha la formulación, se usan valores aleatorios para los
estados iniciales y se actualizan los valores internos y externos de
acuerdo a las ecuaciones de actualización de ![]() y
y
![]() descritas anteriormente, seleccionando la neurona a
actualizar de forma aleatoria.
descritas anteriormente, seleccionando la neurona a
actualizar de forma aleatoria.
Cláramente es difícil expresar problemas de optimización e incorporar las restricciones del problema, además que al seguir un gradiente decendiente es fácil de caer en mínimos locales.