Para GLS: (i) El costo de la solución es la suma de las distancias de los arcos en el ciclo, (ii) los atributos son todos los posibles arcos, (iii) el costo de cada atributo es su distancia, y (iv) a cada arco se le asocia una penalización (inicialmente = 0).
La nueva función de evaluación es:
![]() , donde
, donde ![]() es la distancia,
es la distancia, ![]() es un parámetro y
es un parámetro y ![]() es una matríz de
penalización.
es una matríz de
penalización.
Lo que quiere decir es que cada vez que hagamos un cambio, usando
algún ![]() , tenemos que calcular la distancia total usando
, tenemos que calcular la distancia total usando
![]() y la penalización asociada a cada arco involucrado en el
cambio.
y la penalización asociada a cada arco involucrado en el
cambio.
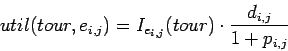
donde
![]() si
si
![]() y es 0 si no
está.
y es 0 si no
está.
Lo único que falta definir es el parámetro ![]() , que
generalmente depende del problema que se quiera resolver.
, que
generalmente depende del problema que se quiera resolver.
Se ha encontrado que buenos valores de ![]() son:
son:
 .
.
En ese caso ![]() es más fácil de sintonizar. Para el agente
viajero se encontró que un rango de
es más fácil de sintonizar. Para el agente
viajero se encontró que un rango de
![]() da buenos resultados.
da buenos resultados.
GLS se puede usar en combinación con otras estrategias.
En particular, la combinación de fast local search con GLS es relativamente directa, solo se tienen que asociar atributos con sub-vecindad.
Por ejemplo, en el TSP se podría tener un bit de activación por ciudad, indicando que ciudades conviene considerar en la vecindad.