11.3 Trazas de Elegibilidad (eligibility traces)

Están entre métodos de Monte Carlo y TD de un paso.

Los métodos Monte Carlo realizan la actualización considerando la secuencia completa de recompensas observadas.

La actualización de los métodos de TD la hacen utilizando únicamente la siguiente recompensa.

La idea de las trazas de elegibilidad es considerar las recompensas de $n$ estados posteriores (o afectar a $n$ anteriores).

Si recordamos:

$$R_t = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \ldots + \gamma^{T-t-1} r_T$$

Lo que se hace en TD es usar:

$$R_t = r_{t+1} + \gamma V_t(s_{t+1})$$

lo cual hace sentido porque $V_t(s_{t+1})$ reemplaza a los términos siguientes ( $\gamma r_{t+2} + \gamma^2 r_{t+3} \ldots$).

Sin embargo, hace igual sentido hacer:

$$R_t = r_{t+1} + \gamma r_{t+2} + \gamma^2 V_t(s_{t+2})$$

y, en general, para $n$ pasos en el futuro.

En la práctica, más que esperar $n$ pasos para actualizar (forward view), se realiza al revés (backward view). Se guarda información sobre los estados por los que se pasó y se actualizan hacia atrás las recompensas (descontadas por la distancia). Se puede probar que ambos enfoques son equivalentes.

Para implementar la idea anterior, se asocia a cada estado o par estado-acción una variable extra, representando su traza de elegibilidad (eligibility trace) que denotaremos por $e_t(s)$ o $e_t(s,a)$.

Este valor va decayendo con la longitud de la traza creada en cada episodio. La figura 11.3 muestra este comportamiento.

Para $TD(\lambda)$:

$$e_t(s) = \left\{ \begin{array}{ll} \gamma \lambda e_{t-1}(s)... ...lambda e_{t-1}(s) + 1 & \mbox{si } s = s_t \end{array}\right .$$

Figura 11.3: Comportamiento de las trazas de elegibilidad.

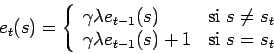
Para SARSA se tiene lo siguiente:

$$e_t(s,a) = \left\{ \begin{array}{ll} \gamma \lambda e_{t-1}(... ...mbda e_{t-1}(s,a) + 1 & \mbox{si } s = s_t \end{array}\right .$$

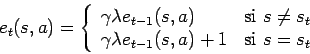
El algoritmo para $SARSA(\lambda )$ viene descrito en la tabla 11.9.

Tabla 11.9: $SARSA(\lambda )$ con trazas de elegibilidad.

Para Q-learning como la selección de acciones se hace, por ejemplo, siguiendo una política $\epsilon-$greedy, se tiene que tener cuidado, ya que a veces los movimientos, son movimientos exploratorios.

Aquí se puede mantener historia de la traza solo hasta el primer movimiento exploratorio, ignorar las acciones exploratorias, o hacer un esquema un poco más complicado que considera todas las posibles acciones en cada estado.