9.1.2 Estrategias Evolutivas

Propuestas en Alemania en 64 para resolver problemas hidrodinámicos complejos.

La versión original (1+1)-EE usaba un solo padre del cual se generaba un solo hijo.

Se mantenia el hijo solo si era mejor que el padre

Un individuo nuevo es generado introduciendo ruido Gaussiano: $\vec{x}_{t+1} = \vec{x}_t + N(0,\vec{\sigma})$, donde $N$ es una vector de números Gaussianos independientes con una media cero y desviación estandar $\vec{\sigma}$.

Por ejempo, supongamos que queremos optimizar: $f(x_1,x_2) = 100(X_1^2 - X_2)^2 + (1 - X_1)^2$ donde, $-2048 \leq x_1,x_2 \leq 2048$.

Ahora supongamos que tenemos el siguiente individuo generado aleatoriamente: (-1,1) y tenemos las siguientes mutaciones:

$$\begin{array}{l} x^{t+1}_1 = x^t_1 + N(0,1.0) = -1.0 + 0.61 ... ...-1,1) = 4 \\ f(x_{t+1}) = f(-0.39,1.57) = 201.416 \end{array}$$

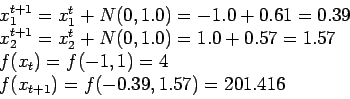
Rechenberg introdujo el concepto de población en donde M padres generan 1 hijo, y Schwefel introdujo el uso de múltiples hijos, pudiendo quedarse con los M mejores hijos o los M mejores individuos considerando a los padres y a los hijos.

Rechenberg también formuló una regla para ajustar la desviación estandar durante el proceso evolutivo para garantizar convergencia, conocida como ``la regla del éxito 1/5'': la razón entre mutaciónes exitosas y el total de mutaciones debe de ser 1/5.

Lo que dice es que la razón entre mutaciones exitosas y el total de mutaciones debe ser 1/5. Si es mayor, incrementa la desviación estandar (divídela entre 0.817), si en menor, decrementala (multiplícala por 0.817).

En las estrategias evolutivas se evoluciona no sólo a las variables del problema, sino también a los parámetros mismos de la técnica (i.e., las desviaciones estándar). A esto se le llama auto-adaptación.