1.1 Ejemplos e Ideas

El problema de las 8 reinas

: El problema consiste en colocar 8 reinas en un tablero de ajedrez sin que se ataquen.

Una posibilidad es intentar lograr una solución de manera incremental, acercándose a la meta poco a poco siguiendo una serie de decisiones locales basadas en la información obtenida durante el proceso.

Hay que asegurarse que la secuencia de transformaciones sea sistemática, para (i) no generar configuraciones repetidas y (ii) no excluir configuraciones deseables.

Una forma de sistematizar la búsqueda es construyendo más que transformando configuraciones (aunque ver GSAT).

Por ejemplo el hecho de que deba de haber sólo una reina por columna nos reduce el número de alternativas a menos de 8 en cada renglón.

El hecho de que podamos sistematizar la búsqueda de esta forma es que no nos podemos recuperar de violaciones a restricciones mediante operaciones futuras. Osea que una vez que violamos una restricción no podemos seguir añadiendo más reinas para rectificarla.

Posibles candidatos de heurísticas:

1. Preferir colocar reinas que dejen el mayor número de celdas sin atacar. En el ejemplo: heu1(A)=8, heu1(B)=9, heu1(C)=10.
2. Ver cuál es el menor número de celdas no atacadas en cada renglón y escoger la que su número menor sea mayor. En el ejemplo: heu2(A)=1, heu2(B)=1, heu2(C)=2

Figura 1.1: El problema de las 8 reinas

La heurística 2 permite detectar caminos sin salida.

El problema del 8-puzzle

: consiste en pasar de una confinguración inicial a una final deslizando cuadros aprovechando el espacio vacío.

Figura 1.2: El problema del 8 puzzle

El tratar de hacer búsqueda exhaustiva es impráctico cuando el número de posibles estados es muy grande, por lo que la decisión de qué hacer depende de una regla o juicio anterior a la búsqueda.

Una posible regla es estimar qué tan cerca se está de la solución.

Algunas heurísticas que se han usado para ésto son:

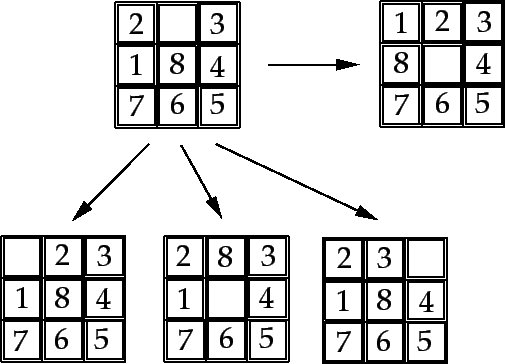
1. Contar el número de cuadros que no corresponden a la meta (sin contar el blanco). En el ejemplo: heu1(A)=2, heu1(B)=3, heu1(C)=4.
2. La suma de la distancia Manhattan de los cuadros que no corresponden a su lugar. En el ejemplo: heu2(A)=2, heu2(B)=4, heu2(C)=4.
3. Distancia del cuadro blanco al primer cuadro fuera de su lugar. En el ejemplo: heu3(A)=1, heu3(B)=1, heu3(C)=3.
4. Distancia entre la posición final del blanco y su posición actual. En el ejemplo: heu4(A)=2, heu4(B)=0, heu4(C)=2.

Encontrar la ruta más corta entre dos ciudades

: dado un mapa con varias ciudades encontrar el camino más corto entre un par de ciudades.

Con el mapa podemos descartar automáticamente rutas poco prometedoras.

Pero si en lugar del mapa se nos dá informacíon de las distancias entre ciudades no es obvia la preferencia.

Esto es porque en el mapa es posible estimar las distancias Euclideanas.

Sin embargo, se pueden calcular las distancias a partir de las coordenadas de las ciudades, por lo que se puede usar esa información extra para determinar que acción tomar, en base a una estimación de lo que falta mas la distancia recorida.

El problema del agente viajero

: encontrar el circuito más corto entre ciudades.

Figura 1.3: El problema del agente viajero

Es un problema NP-duro, por lo que se requiere de heurísticas adecuadas que acoten el problema.

Si tenemos un pedazo de ruta, de las diferentes alternativas que existen en esa ruta la mejor es la que nos estime completar la menor ruta.

Esa estimación puede ser difícil de hacer, pero si es optimísta (subestima consistentemente el costo real) entonces el que nos de la mejor estimación es el mejor.

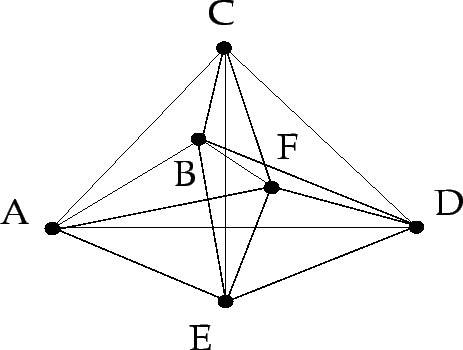
Cuáles pueden ser buenos estimadores sobre los nodos faltantes?

1. El grafo de grado dos más barato (O($n^3$)).
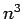2. El árbol de expansión mínimo (O($n^2$)).

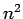Aunque estas aproximaciones no representan ni se asemejan a la solución del poblema, son buenos estimadores.

Algo a considerar, es qué tanto afecta la calidad de los estimadores a la complejidad de la búsqueda.

Detectar la moneda falsa (12 monedas, pesando 3 veces)

: Supongamos que tenemos una moneda falsa (más/menos pesada) en un grupo de 12, una balanza y tres intentos para detectarla.

Se requiere de una estrategia, o sea una descripción de qué hacer primero y en base al resultado obtenido qué hacer después y así sucesivamente.

Se tienen 3 posibles resultados: a) queda balanceado b) se inclina a la derecha y c) se inclina a la izquierda.

Cada acción requiere hacer una estimación de qué hacer para las 3 posibles situaciones. Por lo que el mérito de una acción depende de la combinación de los méritos de las 3 posibles acciones (regla de combinación).

Una vez que se decide alguna alternativa, se necesita especificar qué subproblema tiene que ser considerado después.

Todos estos ejemplos ilustran ideas valiosas como búsqueda incremental, sistemática, el detectar a tiempo caminos sin salida, usar subestimaciones para evaluar posibles alternativas, utilizar información extra, definir estrategias ante posibles resultados de acciones y para cada subproblema, etc.