2.2.3 Búsqueda Bidireccional

Aquí la idea es explorar al mismo tiempo del estado inicial hacia la meta que de la meta hacia el estado inicial hasta que se encuentren en un estado.

Cuando el factor de arborecencia es igual en ambos sentidos, se pueden hacer grandes ahorros.

Puntos a considerar:

• Cuando los operadores son reversibles, los conjuntos de predecesores y sucesores son iguales, pero en algunos casos calcular los predecesores puede ser muy difícil.
• Si hay muchas posibles metas explícitas, en principio se podría hacer la búsqueda hacia atrás a partir de cada una de ellas. Sin embargo, a veces las metas son sólo implícitas (i.e., se tienen una descripción del conjunto posible de estados), lo cual lo vuelve mucho más difícil. Por ejemplo, cuáles son los estados predecesores de una condición de jaque mate en ajedrez?
• Se necesita un método eficiente para revisar si un nuevo nodo aparece en la otra mitad de la búsqueda.
• Se tiene que pensar que tipo de búsqueda hacer en cada mitad (no necesariamente la misma es la mejor).

Para revisar si los nodos se encuentran, por lo menos se tienen que guardar todos los nodos de una mitad (como en breadth-first).

Tabla 2.5: Comparación de algoritmos. 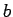$b$ = factor de arborescencia, 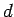$d$ = profundidad de la solución, 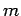$m$ = profundidad máxima, 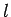$l$ = profundidad límite.

Criterio	Breadth	Costo	Depth	Depth	Itera.	Bidir.
	first	unif.	first	limited	deep.
Tiempo	$b^d$	$b^d$	$b^m$	$b^l$	$b^d$	$b^{d/2}$
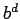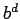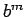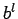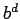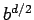Espacio	$b^d$	$b^d$	$b \times m$	$b \times l$	$b \times d$	$b^{d/2}$
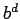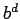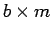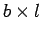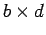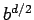Optimo	si	si	no	no	si	si
Completo	si	si	no	si (si 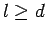$l \geq d$)	si	si