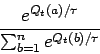11.2.2 Monte Carlo

Next: 11.2.3 Diferencias Temporales (Temporal Up: 11.2 Métodos de Solución Previous: 11.2.1 Programación Dinámica

11.2.2 Monte Carlo

Los métodos de Monte Carlo, solo requieren de experiencia y la actualización se hace por episodio más que por cada paso.

El valor de un estado es la recompensa esperada que se puede obtener a partir de ese estado.

Para estimar $V^{\pi }$ y $Q^{\pi}$ podemos tomar estadísticas haciendo un promedio de las recompensas obtenidas. El algoritmo para $V^{\pi }$ está descrito en la tabla 11.4.

**Tabla 11.4:** Algoritmo de Monte Carlo para estimar $V^{\pi }$ .
$\begin{table} \begin{tabbing} 123\= \kill Repite \\ Genera un episodio usando $... ...mp(s)$\ \\ \> $V(s) \leftarrow$\ promedio($recomp(s)$) \end{tabbing}\end{table}$

Para estimar pares estado-acción ( $Q^{\pi}$ ) corremos el peligro de no ver todos los pares, por lo que se busca mantener la exploración. Lo que normalmente se hace es considerar solo políticas estocásticas que tienen una probabilidad diferente de cero se seleccionar todas las acciones.

Con Monte Carlo podemos alternar entre evaluación y mejoras en base a cada episodio. La idea es que después de cada episodio las recompensas observadas se usan para evluar la política y la política se mejora para todos los estados visitados en el episodio. El algoritmo viene descrito en la tabla 11.5.

**Tabla 11.5:** Algoritmo de Monte Carlo.
$\begin{table} \begin{tabbing} 123\= \kill Repite \\ Genera un episodio usando $... ...odio: \\ \> $\pi(s) \leftarrow \mbox{argmax}_a Q(s,a)$ \end{tabbing}\end{table}$

Existen dos formas para asegurar que todas las acciones pueden ser seleccionadas indefinidamente:

Los algoritmos on-policy: Estiman el valor de la política mientras la usan para el control. Se trata de mejorar la política que se usa para tomar decisiones.
Los algoritmos off-policy: Usan la política y el control en forma separada. La estimación de la política puede ser por ejemplo greedy y la política de comportamiento puede ser $\epsilon$ -greedy. Osea que la política de comportamiento está separada de la política que se quiere mejorar.
Esto es lo que hace Q-learning, lo cual simplifica el algoritmo.

Ejemplos de políticas de selección de acciones son:

$\epsilon-$ greedy: en donde la mayor parte del tiempo se selecciona la acción que da el mayor valor estimado, pero con probabilidad $\epsilon$ se selecciona una acción aleatoriamente.
softmax, en donde la probabilidad de selección de cada acción depende de su valor estimado. La más común sigue una distribución de Boltzmann o de Gibbs, y selecciona una acción con la siguiente probabilidad:

$\begin{displaymath} \frac{e^{Q_t(a)/\tau}}{\sum_{b=1}^n e^{Q_t(b)/\tau} } \end{displaymath}$

donde $\tau$ es un parámetro positivo (temperatura).

Next: 11.2.3 Diferencias Temporales (Temporal Up: 11.2 Métodos de Solución Previous: 11.2.1 Programación Dinámica

Eduardo Morales Manzanares 2004-11-02