La primera versión de ACO se utilizó para resolver el agente viajero.
Al construir soluciones, una hormiga ![]() decide irse de la ciudad
decide irse de la ciudad ![]() a la ciudad
a la ciudad ![]() con la siguiente probabilidad:
con la siguiente probabilidad:
![\begin{displaymath}p_{ij}^{k}(t) = \frac{[\tau_{ij}(t)]^{\alpha} \cdot
[\eta_{i...
...a}
\cdot [\eta_{ij}]^{\beta} } \mbox{ si } j \in {\cal N}_i^k \end{displaymath}](img478.png)
donde
![]() es información disponible,
es información disponible, ![]() y
y ![]() son parámetros que se tienen que definir, y
son parámetros que se tienen que definir, y ![]() es la vecindad factible de la hormiga
es la vecindad factible de la hormiga ![]() (el conjunto de ciudades que
(el conjunto de ciudades que
![]() no ha visitado).
no ha visitado).
Si ![]() se visita la ciudad más cercana. Si
se visita la ciudad más cercana. Si ![]() se
basa solo en las trazas de feromona y tiende a converger rápidamente
a un punto de no mejora subóptimo.
se
basa solo en las trazas de feromona y tiende a converger rápidamente
a un punto de no mejora subóptimo.
Cuando todas las hormigas completan un circuito, se actualizan las
feromonas.Primero se reducen todos los caminos por un factor constante
(evaporación) y después cada hormiga deposita la siguiente cantidad
de feromona en los nodos de su circuito:
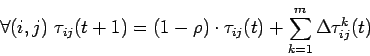
donde
![]() es la razón de evaporación de feromona y
es la razón de evaporación de feromona y
![]() es el número de hormigas.
es el número de hormigas.
![]() es la cantidad que deposita cada hormiga en
cada nodo, definida por:
es la cantidad que deposita cada hormiga en
cada nodo, definida por:
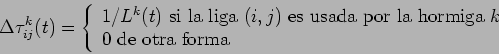
donde ![]() es la longitud del circuito de la hormiga
es la longitud del circuito de la hormiga ![]() .
.