Modelos Gráficos Probabilistas
Problemas
Probabilidad
1. Alguien tiene una, y sólo una, de
dos
posibles
enfermedades: influenza (I) o gripe (G). Hay dos posibles
síntomas: dolor
de cabeza
(D)
y fiebre (F), cada uno de los cuales puede ser verdadero (D, F) o falso
(~D, ~F). Dados:
P(I) = 0.6
P(D|I) = 0.7
p(D|~I) = 0.4
P(F|I) = 0.9
P(F|~I) = 0.5
Asumiendo que los síntomas son
independientes dada la enfermedad:
a) Describe el espacio de muestreo
b) Completa
las tablas de probabilidad.
b) Obten la probabilidad de que alguien tenga
influenza
dado que no tiene dolor de cabeza y tiene fiebre.
Teoria de
Informacion
2. En cierto lugar el clima se comporta
estadisticamente
de la siguiente manera: de 365 dias, 200 lluvia, 60 nublados, 40 sol,
20
nieva, 20 tormenta, 10 graniza, 10 viento y 5 llovizna
a) Si cada dia se envia un mensaje con el
clima,
que informacion da para cada tipo de clima?
b) Cual es el promedio de bits de informacion
que da el mensaje?
Grafos
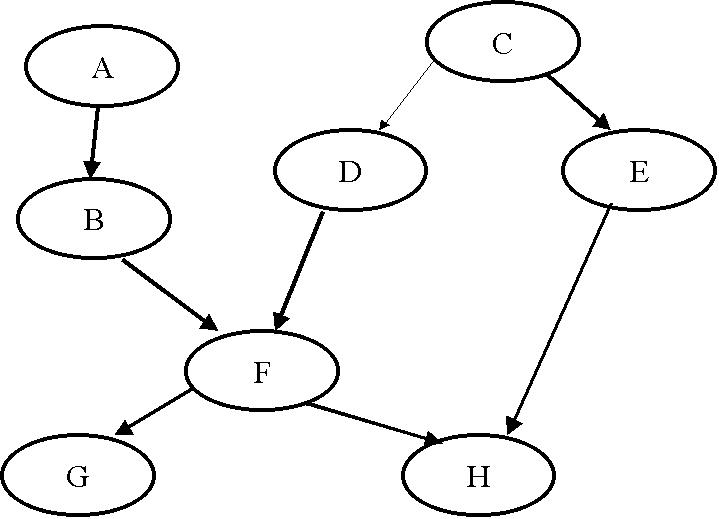
3. Para el grafo de la figura:
a) ordena los nodos de acuerdo a maxima
cardinalidad
b) triangula el grafo
c) determina los cliques
d) ordena los cliques y verifica la propiedad
de intersección secuencial
e) muestra el árbol de cliques resultante
Métodos
Básicos y Clasificadores
4. Dada la siguiente tabla de datos:
| Ambiente |
Temperatura |
VIENTO |
JUGAR |
| S |
A |
N |
N |
| S |
A |
S |
N |
| N |
A |
N |
S |
| L |
M |
N |
S |
| L |
B |
N |
S |
| L |
B |
S |
N |
| N |
B |
S |
S |
| S |
M |
N |
N |
| S |
B |
N |
S |
| L |
M |
N |
S |
| S |
M |
S |
S |
| N |
M |
S |
S |
| N |
A |
N |
S |
| L |
M |
S |
N |
Obtener:
a) La tabla de probabilidad conjunta (para todas las combinaciones de
valores de las variables).
A partir de las probabilidades
conjuntas, determinar:
b) Las probabilidades marginales de jugar y
ambiente
c) La probabilidad de Jugar dada Temperatura=M
d) El valor de mayor probabilidad de Jugar dado
Temperatura
e) A partir de los datos, obtener las tablas de probabilidad
requeridas para construir un clasificador bayesiano simple para Jugar
Práctica de
Clasificadores
5. Utilizar uno de los conjuntos de UC Irvine ML Repository
(sugiero seleccionar un conjunto de datos con "pocos" atributos, si los
atributos son continuos, discretizarlos con el mismo Weka) para obtener
clasificadores
bayesianos (Naive Bayes y TAN) en WEKA
y analizar los resultados:
a) Comparar los resultados utilizando
diferentes opciones de prueba (test options)
b) Visualizar los modelos obtenidos y los parámetros
c) Analizar y comentar los resultados con ambos modelos
Hacer un breve reporte
(máximo 3 páginas) que incluya lo siguiente:
- Un breve descripción de
las pruebas
realizadas, los resultados y su análisis
- Gráficas de
los clasificadores generados (NB y TAN)
Modelos
Ocultos de Markov
6. Para el ejemplo del HMM de dos monedas
cargadas
(de la clase) y considerando la secuencia de observaciones AASS,
calcular:
a) Probabilidad
de la secuencia por el método
directo
b) Probabilidad de la secuencia por el método iterativo
b) Comparar el número de
operaciones en (a) y (b)
c) Estimar la secuencia de estados más
probable
(algoritmo de Viterbi)
Campos de
Markov
7.
Considerar un CAM de primer orden de 4 x 4
sitios, donde cada sitio puede tomar los valores [0,1]. Considerando
una
configuración inicial de ceros en todos los sitios, una cierta
observación
(figura) y una lambda = 4 (mayor peso a las observaciones), utiliza los
potenciales de suavizamiento para
obtener los valores del campo para dos iteraciones
del algoritmo ICM.
Observacion (G):
| 0 |
0 |
0 |
0 |
| 0 |
1 |
1 |
1 |
| 0 |
1 |
0 |
1 |
| 0 |
1 |
1 |
1 |
Redes
Bayesianas - representación
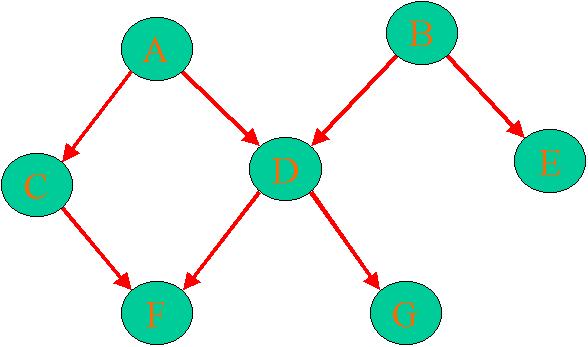
8. Para la red bayesiana de la figura:
a) Identifica el Contorno de Markov de cada nodo
y escribe la ecuación para la probabilidad conjunta.
b) Identifica la Cobija de Markov de cada nodo.
c) Di si las siguientes relaciones son verdaderas o falsas y
porqué: I(C,A,D), I(A,CD,F), I(C,F,D), I(A,D,BE),
I(A,DB,G), I(E,D,B), I(A,G,B), I(A,DG,B)
d) A partir de las relaciones de independencia en (c), deduce otras aplicando los axiomas
Redes
Bayesianas - inferencia
9. Para la red bayesiana del ejemplo de
propagación en árboles (visto en clase), considera que la
única evidencia es que comida=insalubre
(2do valor):
a) Obten las condiciones iniciales para este caso
b) Realiza el cálculo de probabilidades de las demás
variables en la RB mediante el método de propagación en
árboles, muestra el procedimiento.
c) Obten la probabilidad de la variable "Dolor" mediante el método de eliminación.
Práctica de Aprendizaje de Redes Bayesianas
10. Utiliza los datos completos del ejemplo de "golf" visto en clase para:
a) Obtener la información mutua entre todos los pares de variables
b) Construir el árbol óptimo de acuerdo al algoritmo de Chow & Liu
c) Determinar la dirección de los arcos mediante las pruebas de independencia entre tripletas de variables
d) Aprender una red bayesiana utilizando la herramienta Hugin (bajar versrón gratuita)
e) Contrastar el árbol aprendido vs. la red con Hugin
Entregar un reporte cubriendo los 5 incisos, incluyendo los modelos aprendidos

